Calculus: How to use calculus for better gameplay

Most of you reading this post know what deltaTime is, and you know to multiply things by it to make your game framerate independent. Or, rather, most of you think you are making your game framerate independent by doing that.

The bad news is, for most things just multiplying by DT won't be enough. The good news is, we get to use a bit of calculus to gain actual framerate independence! Well... Maybe that's bad news for a lot of you. I think it's spectacular news (˵ ͡° ͜ʖ ͡°˵)

Cat with gun meme

This isn't optional either. Stand down calmly and pay attention, or meow-meow is gonna have to deal with you.

Very well! Let's begin!

Constant Velocity and DT

What we have below is something you should already be pretty familiar with. The simplest example: An object moving at constant speed. You can adjust the framerate, as well as the movement speed of the circles. Each circle has a reference next to it, designated by the same color at lower saturation. These references are always updated at 60 fps.

The blue circle is simply moving a constant amount based on its speed every frame. The result is, of course, that it moves faster as framerate increases. If the stepsize is constant, more steps per second means more distance covered.

The red circle multiplies by Delta Time. That is, the time elapsed since the last frame. If we update at 10 FPS, and our frames are consistent in time, that will give us a Delta Time (DT) of 0.1. This, in turn, means that our speed value is now equivalent to "distance per second".

Play around with the slider for a bit. You'll notice the red circles stay in sync regardless of framerate or speed values. The blue circles diverge over time. At higher speed or framerate values, they diverge even faster.

Even in this simple case, there's a subtle error one could make. It comes from the behavior of bouncing back and forth. In the frames where a circle reaches its end position, it'll often have some "leftover" movement. If it was going to move 7 units, but was 3 units away from its final position, it would still have to move 4 more units after changing direction, in the same frame.

If it doesn't do that, and instead stops at its position regardless of the leftover movement, the two circles will diverge in their position over time. This is because the size of the residual movement will, on average, be larger at lower framerates.

// INCORRECT - Truncates leftover movement
void UpdatePosition() {
    position += direction * speed * Time.deltaTime;
    
    if (position <= 0) {
        position = 0;  // Truncates overshoot!
        direction = 1;
    } else if (position >= maxHeight) {
        position = maxHeight;  // Truncates overshoot!
        direction = -1;
    }
}

// CORRECT - Handles leftover movement
void UpdatePosition() {
    position += direction * speed * Time.deltaTime;
    
    if (position <= 0) {
        float overshoot = -position;
        position = overshoot;  // Bounce with overshoot
        direction = 1;
    } else if (position >= maxHeight) {
        float overshoot = position - maxHeight;
        position = maxHeight - overshoot;  // Bounce with overshoot
        direction = -1;
    }
}

You can enable the "Truncate Bounce" mode to see this. The circles will diverge from their reference a bit more with each bounce. At lower framerate and higher speeds the error will accumulate much faster.

So, even in the simple case there's errors you could make. Even here, it's worth thinking about. But, things get more complicated. Let's go to an example where the "just multiply by DT" rule-of-thumb fails to give us the right result.

Acceleration

In our last example, speed was a constant. Now, it is also something that changes over time.

Just multiplying our movement by DT obviously gives us the wrong result, since the change in speed will be framerate-dependent. As expected, the red circle and its reference quickly diverge.

So, let's just multiply acceleration by DT as well. That should do the trick! The change in our position is made framerate-independent, and the change in our speed is made framerate independent. This is what the green circles are doing:

If you give it a bit of time, you'll notice that the green circle and its reference are still diverging over time. The divergence happens faster at lower framerates and/or higher acceleration values.

The purple version does something different. The same divergence isn't happening for it. We'll go over what it does differently in a little bit. But first, why isn't multiplying both acceleration and movement by DT enough?

This is where the calculus comes in.

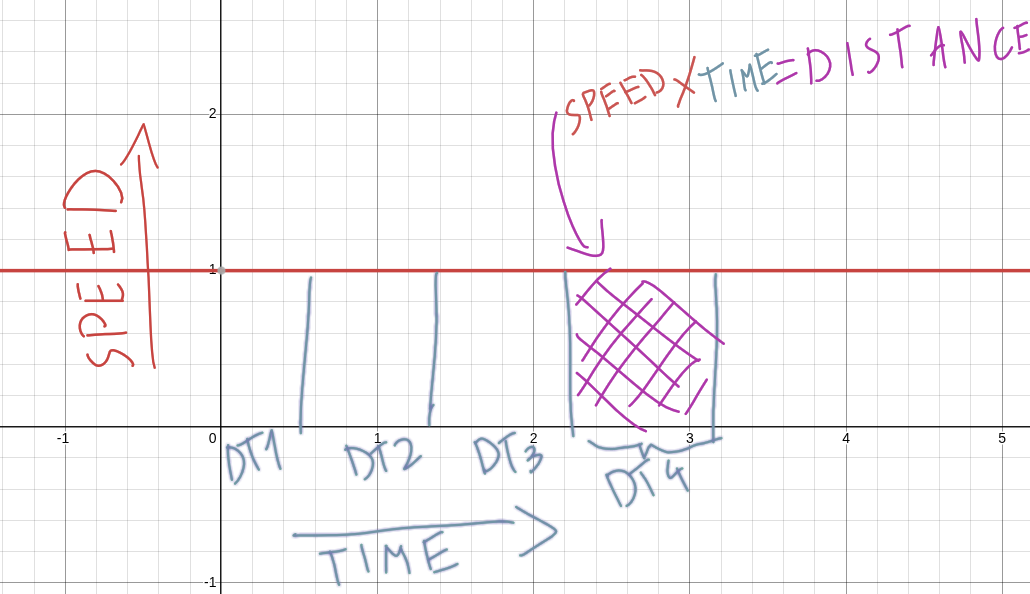
Graph showing constant velocity over time

We're out of cool visualizations, so it's shoddy drawings I made from here on out.

What we have above is a graphed out function representing our speed over time in the first example. The X axis is time, the Y axis is our speed. Since our speed was constant, it is a straight line, it doesn't change with time. The X-axis is broken up into DT chunks, these are the chunks of time we actually get to work with in our game.

So, it becomes pretty easy to see what we have to do to calculate our movement over a specific frame of length DT. If we define our speed as just distance/second, and our DT is measured in seconds, then we just have to do some simple math to calculate our movement.

$$\left(\frac{\text{distance}}{1 \text{ second}}\right) \times \text{DT seconds} = \text{distance moved over DT time}$$

When graphed out we can see how this translates nicely to geometry! We're just calculating the area of a rectangle. Time is the width, speed is the height, area is just width × speed.

That is what we are doing when we multiply by DT.

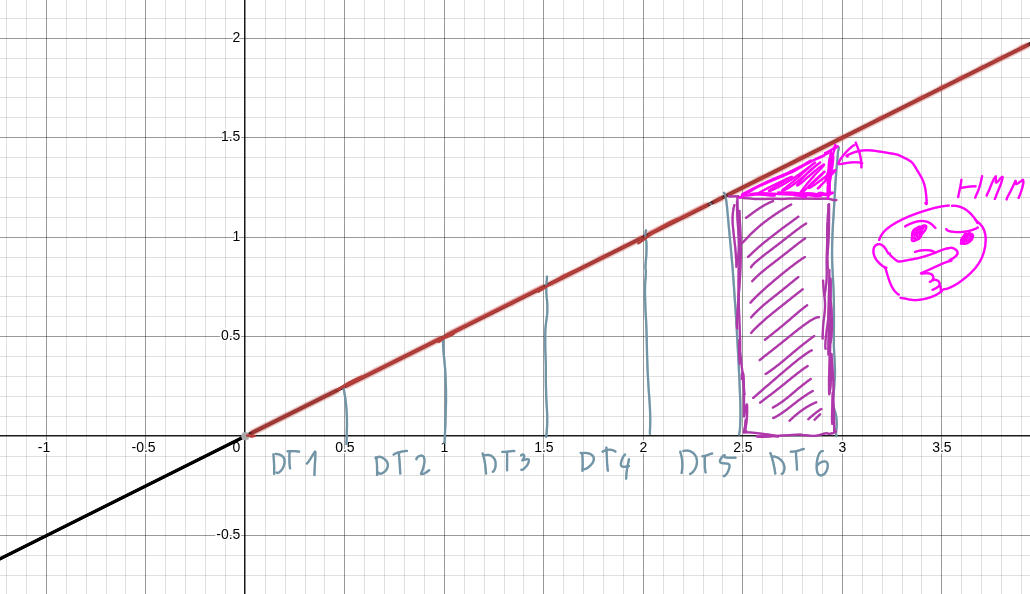
Graph showing linear acceleration over time

Now, let's take a look at what is happening in our second visualization. Our speed now starts at 0, and increases linearly. So, let's graph out that new function.

Our goal is the same as before. The amount of distance we have to move is equal to the area of the shape underneath our function, between time T and T + DT.

What changed is that shape is no longer a rectangle! What we have is more like a rectangle, and then a right triangle on top of it. With some pen and paper, you could still calculate that area pretty easily using some basic geometry.

But, part of the fun of math is there are many methods to achieve the same thing. Calculating "Area under a function" is in fact exactly what integrals do. What we actually want is a bit different: "Area under a function between two specific points on the X axis"; Definite integrals do exactly that!

Developing an understanding for *why* integrals can do that is probably good, but not entirely necessary. For our current purposes, we will gloss over why this works. If you do want to learn the why, I've added some useful links at the bottom of the page.

As for, how do you actually solve an integral, there's a few different answers. The easy path is: Just stick it into one of the many tools that can solve them for you. I like Wolfram Alpha. You just copy paste the integral in, and it'll probably be able to give you a solution. The harder path is: You learn how to do it yourself. For simple integrals, there's a few basic formulas that will just give you the answer. Beyond that, there's a few basic rules that can allow you to decompose more complex integrals into simpler ones. For example: Substitution, integration by parts, etc.

For most of your game development purposes, using a tool to get the right answer will be good enough. The critical skill is to be able to correctly formulate the problem, that's the prerequisite for being able to use a tool like Wolfram Alpha.

Anyways, so back to our example. Here's how you compute a definite integral:

$$\int_a^b f(x) \, dx = F(b) - F(a)$$

where F(x) is the antiderivative (integral) of f(x)

And now here's our specific example:

$$\text{For velocity function: } v(t) = a \cdot t$$ (where a is acceleration)

$$\text{Distance} = \int_T^{T+\text{DT}} a \cdot t \, dt = \frac{a \cdot t^2}{2} \Big|_T^{T+\text{DT}}$$ $$= \frac{a \cdot (T+\text{DT})^2}{2} - \frac{a \cdot T^2}{2}$$ $$= \frac{a}{2}(T^2 + 2T \cdot \text{DT} + \text{DT}^2) - \frac{a \cdot T^2}{2}$$ $$= a \cdot T \cdot \text{DT} + \frac{a \cdot \text{DT}^2}{2}$$

This gives us the correct formula for updating our position: position += acceleration x Time × DT + 0.5 × acceleration × DT²

Time is the time we've been accelerating for until the start of last frame. In other words, acceleration x Time is just our velocity at the start of last frame

So, we can simplify our formula to: position += old_velocity × DT + 0.5 × acceleration × DT²

This is what the purple circle in our visualization is using.

Here's how you'd implement this in code:

// Correct physics for constant acceleration
                void UpdatePositionWithAcceleration() {
                    float dt = Time.deltaTime;
                    
                    // Store the velocity at the start of this frame
                    float oldVelocity = velocity;
                    
                    // Update velocity (acceleration changes velocity over time)
                    velocity += acceleration * dt;
                    
                    // Update position using the correct physics formula
                    // This accounts for the changing velocity during the frame
                    position += oldVelocity * dt + 0.5f * acceleration * dt * dt;
                }

Let's take a look at a slightly more complex example, where our velocity goes up exponentially:

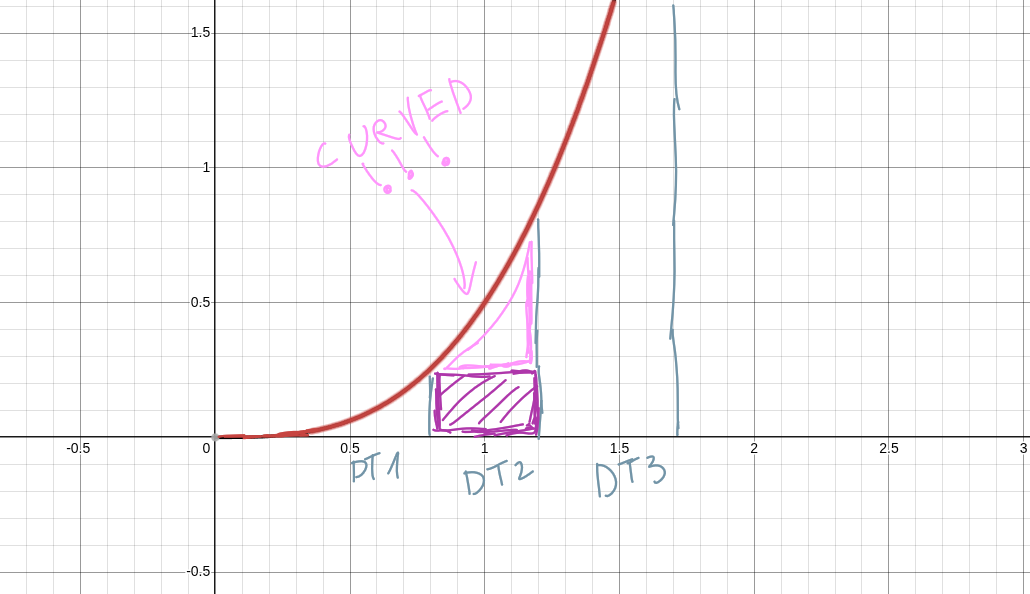
Graph showing more complex velocity function

Here, our acceleration function is:

$$ v(t) = a * t^3$$

Our acceleration is now rising at an exponential rate! Cubically, to be precise! Unlike the last example, there's no basic geometry alternative. Fortunately, the calculus solution is pretty much just as simple! The only thing that has changed is our speed function. We're just integrating this new function. It is a simple one.

$$\text{Distance} = \int_T^{T+\text{DT}} a \cdot t^3 \, dt = \frac{a \cdot t^4}{4} \Big|_T^{T+\text{DT}}$$ $$= \frac{a \cdot (T+\text{DT})^4}{4} - \frac{a \cdot T^4}{4}$$ $$= \frac{a}{4}(T^4 + 4T^3 \cdot \text{DT} + 6T^2 \cdot \text{DT}^2 + 4T \cdot \text{DT}^3 + \text{DT}^4 - T^4)$$ $$= a \cdot T^3 \cdot \text{DT} + \frac{3a \cdot T^2 \cdot \text{DT}^2}{2} + a \cdot T \cdot \text{DT}^3 + \frac{a \cdot \text{DT}^4}{4}$$

That again, gives us the correct formula for updating our position:

position += old_velocity × DT + 1.5 × a × T² × DT² + a × T × DT³ + 0.25 × a × DT⁴

Here's how you'd implement this in code:

// Correct physics for cubic velocity function v(t) = a * t³
                void UpdatePositionWithCubicVelocity() {
                    float dt = Time.deltaTime;
                    
                    // Current time since movement started
                    float T = timeSinceStart;
                    
                    // Calculate velocity at start of frame: v = a * T³
                    float oldVelocity = accelerationConstant * T * T * T;
                    
                    // Update position using the integrated formula
                    position += oldVelocity * dt 
                            + 1.5f * accelerationConstant * T * T * dt * dt
                            + accelerationConstant * T * dt * dt * dt
                            + 0.25f * accelerationConstant * dt * dt * dt * dt;
                    
                    // Update time for next frame
                    timeSinceStart += dt;
                    
                    // For small dt values, you can often ignore the higher-order terms:
                    // position += oldVelocity * dt + 1.5f * accelerationConstant * T * T * dt * dt;
                    // their contribution to the error will be tiny. The amount of accuracy you actually need varies a lot.
                }

Why Bother?

Some would argue that the approximate solutions are good enough, people don't care and can't notice that your game isn't mathematically perfect. Who cares if everything has a few units of error over time.

I would say, if everything accumulated a few units of error over time in the same way, then it wouldn't matter. That isn't what happens in practice. Each one of your functions will accumulate error in different patterns and at different rates.

In practice, this translates to different game systems accumulating error at different rates across framerate variations. Perhaps your walking stays consistent, while your sprint gains higher acceleration at higher framerates. Your jump becomes a bit shorter as your framerate increases, and a bit longer as it decreases. Your dodge-roll feels more bursty and covers a shorter distance as your framerate goes up, and it feels floatier but reaches further as your framerate goes down.

Essentially none of your players are going to be able to articulate things like that. You won't get a playtester that will report these inconsistencies to you. At best, maybe you'll get some vague acknowledgement that some of your systems "feel" wrong.

You shouldn't confuse that difficulty in articulating the problem to mean that there is no problem. The players do notice. In fact, most of what players notice about your game isn't something they can articulate.

If you don't believe that, take a different example. You've probably worn many pairs of shoes in your life; Some you've experienced as being more comfortable, others less-so. If someone were to ask you what exactly determined your experience, you probably wouldn't be able to articulate any of the details. The details are there, and if you spent enough time examining your own experience you'd start to find them.

That being said, not every single detail is important, of course. Some systems do just fine with simple approximations. They don't need that much consistency.

The important parts are:

  1. Being aware of when you are using an approximation, as opposed to the mathematically correct code.
  2. Testing your game across very different framerates, and obsessing over the details. Does your dodge roll feel the same at 30fps and at 60fps? Does it cover the same distance? Does it take the same amount of time to complete? If you're able to verify that all of the above are true, you probably have a good enough solution. If some of the above aren't true, then you'll have the tools to make it so.
  3. Anything where error accumulates over time, you should probably get an exact solution for.

Game Feel

In my opinion, the above problem falls under the umbrella of Game Feel. I think by now there's broad agreement in the game development community that Game Feel is an important part of games. What is currently lacking, for the most part, is a concrete understanding of what Good Game Feel actually entails.

For the most part, it's still a field made up of mostly tacit knowledge. Each developer has their own bag of tricks, and develops their own unspoken intuition to guide them. Currently, it is almost all art, and almost no science.

That's not really a good thing though. Mixing a bit of science into the art often leads to great results. That is a big part of what happened in the Renaissance.

Medieval art example

Medieval

Renaissance art example

Renaissance

That is a big part of what separates the two images above. A common foundation of perspective, anatomy, optics, proportions. A foundation made not of art, but of science and reliable rules. That foundation didn't stifle art and creativity. It led to, well, a renaissance of creativity. More ambitious and profound works became possible, because of a stable foundation. Even abstract modern art was ultimately able to evolve by standing on top of that same foundation, and making deliberate decisions to deviate from it in interesting ways.

I think a bit of basic calculus is one of those foundational tools for game feel. Consistency and accuracy across different framerates is far from the only way we can apply calculus for Game Feel.

In the followup to this post I'll talk about how I built the knockback system for The Bleak Divine. There, we will build a knockback system for a 2D Souls-Like platformer that:

  1. Always covers an exact, configurable distance. This can be any number we pass in at runtime.
  2. Always takes an exact, configurable time to complete. This can also be any number we choose at runtime.
  3. Isn't a linear movement, but rather uses a nice falloff-curve; Fast at the beginning of the movement, slows down to a standstill towards the end.

Links: